The first body in the solar system is the sun.
It is a ball of plasma, it's radius is 109.2 times larger than earth. It accounts for 99.86% of the total mass of the Solar System. It's surface gravity is 28 times earth's.
Now, on to the facts that really make the difference to our human, house, boat, and airplane.
The surface temperature is 5,800 K. That's 9980.33 °F or 5526.85 °C.
How hot is that?
What? What was that? You want me to write something? Sorry. Just getting lost in youtube.
Essentially, plasma is fire:
So, what would happen to anything on the surface of the sun? Well, around 5800K, carbon atoms are ripped apart.
First, the gravity:
The sun has 28 times the gravity of the earth. A typical person can stand about 5g before losing consciousness, and with training and specialized clothing you could withstand 9g. However, at 28g you would not even be able to stand. You would quickly be killed, if only by the fact the the heart is not strong enough to pump blood around your body at 28g. The heat would kill you, quickly, but sometime after a nanosecond. Because of the heat in the sun, photons would have very short wavelengths. Those would ionize your DNA, which is not good. Cancer is the least of your problems.
I think that our building could theoretically stand up, especially with reinforcements, since a 1 story house would only weigh about as much as a 28 story house, which is perfectly possible on earth. In fact, it could be more stable than a 28 story house, since it's closer to the ground, and therefore more stable. Too bad it's rapidly being converted to plasma by heat and radiation which rips apart the very molecular bonds inside the walls.
Similar things happen to the airplane and the boat, and since there's no oceans or atmosphere high enough for the plane to not be vaporized, they're not very interesting.
At the very least, you might trigger a solar flare: http://meetings.copernicus.org/www.cosis.net/abstracts/EGU05/04384/EGU05-J-04384.pdf
See you on Mercury!
Saturday, August 29, 2015
Thursday, August 27, 2015
The size of space
Space is big. Really big. You just won't believe how vastly, hugely, mind-bogglingly big it is. I mean, you may think it's a long way down the road to the chemist, but that's just peanuts to space.-Douglas Adams
Space is as infinite as we can imagine, and expanding this perspective is what adjusts humankind’s focus on conquering our true enemies, the formidable foes: ignorance and limitation.-Vanna Bonta
Today we have an interesting topic; How big is the solar system?
You might be familiar with maps of the solar system like this:
But if you want to know really how big the solar system is, take a look at this map, with the moon the size of a pixel, and everything else to scale: http://joshworth.com/dev/pixelspace/pixelspace_solarsystem.html
If you have 297 minutes, you can travel it at the speed of light. Or, perhaps, 177,632,973,808.5 Blue Whales
Such misconceptions run rampant, as shown here: https://www.youtube.com/watch?v=Bz9D6xba9Og
Next, take a look at the 70's classic short scientific film: Powers of ten
For the more interactive of you, here's a fascinating scrollable scale from the planck length to the observable universe. There's some interesting stuff in there, for example: A marathon is longer than Phobos.
So, yes. Space is truly massive and almost empty. Remember, any solar system is incredibly dense by cosmic standards. Want to explore it yourself? See Celestia For a example of the challenges in spaceflight, take a look at Kerbal Space Program If you are playing Kerbal Space Program and feeling a lack of challenge, try the Realism Overhaul modification.
Now that you know how big space is, you can see how many humans are in it right now. And then watch this awe-inspiring video: http://www.erikwernquist.com/wanderers/
So, why all this preamble? Because I'm going to start a series of posts on what would happen if a plane, a boat, a human, and a building were transported to every large body in the solar system.
Invaluable for this will be What If's posts Interplanetary Cessna and Extreme Boating
See you on the sun, with a 747, a condo, and a sailboat.
P.S.
I was recently linked to by the blog Way Of The Dodo
Tuesday, August 25, 2015
Launch alert! GSLV Mk. 2 • GSAT 6
The Indian Space Research Organization (ISRO) will be launching a GSLV into geosynchronous orbit with a GSAT as the payload. It will launch from Satish Dhawan Space Center, Sriharikota, India. The GSAT is a communications satellite which will used for digital audio, data and video broadcasting.
Download mission brochure.
The launch was a success.
Download mission brochure.
The launch was a success.
Sunday, August 23, 2015
Curiosity on Mars

Today we have a picture of the rover Curiosity on Mars.
This picture was taken by a camera on the end of Curiosity's robotic arm, the camera is designed to take close-up images of details on rocks, but it can also rotate to image the rover itself. It took many pictures, which were stitched back together after they were transmitted back to earth. Only the shadow of the robotic arm is visible because it can rotate out of the image area.
Saturday, August 22, 2015
Thrust to weight ratio
Readers,
Today we have another post on rocket science concepts, thrust to weight ratio! (Yes, I play Kerbal space program, if you haven't already guessed.)
Thrust to weight ratio (let's call it TWR from now on) is a concept in rocketry. It is how much thrust the rocket has to how heavy it is. If you have engines totaling 100 pounds of thrust, and 100 pounds of rocket (Including engines) you will have a earth TWR of 1. That means that at sea level, your rocket will hover, exerting no force upon the ground (aside from the rocket exhaust quickly making a crater), but appearing to rest on it. As the fuel inside your 100 pound rocket burns, your TWR slowly increases, and you begin to rise slowly. Because of the natural logarithm, your rocket will rise faster as it burns fuel. Also, as it rises, there will be slightly less gravity exerting it's force on it, and it will rise faster.
Here's the math:

This formula is more simple, and only requires this to be understood: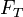 is the thrust of the engine,
is the thrust of the engine,  the total mass of the craft, and
the total mass of the craft, and  is the local gravitational acceleration (usually surface gravity).
is the local gravitational acceleration (usually surface gravity).
The unladen mass of a rocket engine is generally very high, since it needs to lift all that fuel. Wikipedia has a nice table on that.
TWR can be calculated for anything, for example, airplanes, machine guns, sci-fi, and video games:
(Note that the math for surface acceleration is definitely not guaranteed for earth rockets)
Today we have another post on rocket science concepts, thrust to weight ratio! (Yes, I play Kerbal space program, if you haven't already guessed.)
Thrust to weight ratio (let's call it TWR from now on) is a concept in rocketry. It is how much thrust the rocket has to how heavy it is. If you have engines totaling 100 pounds of thrust, and 100 pounds of rocket (Including engines) you will have a earth TWR of 1. That means that at sea level, your rocket will hover, exerting no force upon the ground (aside from the rocket exhaust quickly making a crater), but appearing to rest on it. As the fuel inside your 100 pound rocket burns, your TWR slowly increases, and you begin to rise slowly. Because of the natural logarithm, your rocket will rise faster as it burns fuel. Also, as it rises, there will be slightly less gravity exerting it's force on it, and it will rise faster.
Here's the math:

This formula is more simple, and only requires this to be understood:
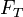 is the thrust of the engine,
is the thrust of the engine,  the total mass of the craft, and
the total mass of the craft, and  is the local gravitational acceleration (usually surface gravity).
is the local gravitational acceleration (usually surface gravity).The unladen mass of a rocket engine is generally very high, since it needs to lift all that fuel. Wikipedia has a nice table on that.
TWR can be calculated for anything, for example, airplanes, machine guns, sci-fi, and video games:
(Note that the math for surface acceleration is definitely not guaranteed for earth rockets)
Friday, August 21, 2015
InSight lander
Get frequent flier miles with NASA!
Put your name on a list of names which will be on a microchip on the InSight mars lander when it lands on the red planet on September 28, 2016.
The InSight lander is a probe similar to the 2007 phoenix lander, but this one has several new instruments intended to find out about the early geologic history of Mars.
Put your name on a list of names which will be on a microchip on the InSight mars lander when it lands on the red planet on September 28, 2016.
The InSight lander is a probe similar to the 2007 phoenix lander, but this one has several new instruments intended to find out about the early geologic history of Mars.
Thursday, August 20, 2015
Welcome to Delta-V!
Hello, Readers!
This is my blog on rocket science, astronomy, and spaceflight! I will post interesting space news for your entertainment.
The name of my blog, Delta-V, comes from the basic piece of math from which most rocket science is based; The Tsiolkovsky rocket equation. Which is, quite simply, a way of finding out how far a rocket could get, in a perfect universe. It looks like this:
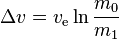
It's named after Konstantin Tsiolkovsky, just so you know.
Don't worry, it's not as bad as it looks.
Let's unpack it. First, moving from the left to the right, we have this symbol: Δv It is pronounced delta-vee. That is the mathematical way of describing change in velocity. If a spacecraft has a Delta-V of 1,200m/s, then, if it was in a gravity free vacuum, it would be traveling at 1,200m/s after it had burned all of it's fuel.
Now, we have the rest of the equation, starting with , which is the effective exhaust velocity. In other words, how fast the exhaust from the rocket comes out. The faster it comes out, the more efficient the rocket is.
, which is the effective exhaust velocity. In other words, how fast the exhaust from the rocket comes out. The faster it comes out, the more efficient the rocket is.
Then there's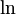 , which is the natural logarithm, and that accounts for the fact that the rocket accelerates faster as it uses up fuel.
, which is the natural logarithm, and that accounts for the fact that the rocket accelerates faster as it uses up fuel.
Finally, to factor in the mass fraction, which is how much fuel mass to ship mass there is in the ship. If it's higher, there is more "stuff" to be used for propellant.
If you add it all together, you get a formula which can tell you how far your rocket can go.
And here are some people who explain it better than I:
Wikipedia
Randall Munroe
William Greene
Don Pettit
This is my blog on rocket science, astronomy, and spaceflight! I will post interesting space news for your entertainment.
The name of my blog, Delta-V, comes from the basic piece of math from which most rocket science is based; The Tsiolkovsky rocket equation. Which is, quite simply, a way of finding out how far a rocket could get, in a perfect universe. It looks like this:
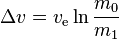
It's named after Konstantin Tsiolkovsky, just so you know.
Don't worry, it's not as bad as it looks.
Let's unpack it. First, moving from the left to the right, we have this symbol: Δv It is pronounced delta-vee. That is the mathematical way of describing change in velocity. If a spacecraft has a Delta-V of 1,200m/s, then, if it was in a gravity free vacuum, it would be traveling at 1,200m/s after it had burned all of it's fuel.
Now, we have the rest of the equation, starting with
 , which is the effective exhaust velocity. In other words, how fast the exhaust from the rocket comes out. The faster it comes out, the more efficient the rocket is.
, which is the effective exhaust velocity. In other words, how fast the exhaust from the rocket comes out. The faster it comes out, the more efficient the rocket is. Then there's
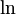 , which is the natural logarithm, and that accounts for the fact that the rocket accelerates faster as it uses up fuel.
, which is the natural logarithm, and that accounts for the fact that the rocket accelerates faster as it uses up fuel.Finally, to factor in the mass fraction, which is how much fuel mass to ship mass there is in the ship. If it's higher, there is more "stuff" to be used for propellant.
If you add it all together, you get a formula which can tell you how far your rocket can go.
And here are some people who explain it better than I:
Wikipedia
Randall Munroe
William Greene
Don Pettit
Subscribe to:
Posts (Atom)
